As you may know, producing good quality random numbers is far from easy – yet they are incredibly important. Random numbers protect every cryptographic operation and many security foundations rely on random numbers being really random.

But how can a computer who “stupidly” follows a pre-defined program create random numbers? Well, the answer is it can’t and that’s why most of them are called Pseudo-Random-Number generators. They take a “random” seed and come up with a deterministic way to create random numbers from that… But if you know the seed, you know all the random numbers!

To create better random numbers, you need to take effects outside of a computer program into account (such as atmospheric noise, quantum tunneling, …)

But Quantum Computers can actually produce “perfect” random numbers, and in this blog post I want to illustrate why that’s the case and also show what the results coming from a real Quantum Computing architecture looks like.

How to produce perfect random numbers with QC?

It is actually surprisingly simple. You take one qubit and bring it into an equal “superposition” between 0 and 1 (basically exactly half-way in between 0 and 1) by applying the Hadamard Gate.

 

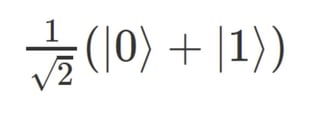
Why is that so cool?

Without having to know all the nitty gritty details, it means that the outcome of a measurement is exactly 50/50 (meaning it is “0” in exactly 50% of the cases and “1” in exactly 50% of the cases. A perfect coin-toss. No bias, no cheating, no algorithm, no see, exactly 50/50 distribution and each random bit is independent of the others, which will give us exactly what we want. Yay 🙂

 

Let’s use this to create lots of random numbers

Ok, so to take this 1 bit to a byte, I’ll repeat this 8 times. And then I’ll repeat this over and over again to collect some random numbers that I can analyze.

I wanted to use the 14 Qubit Quantum Computer from IBM Q for this experiment, but it would not give me the raw values and just counts, so I had to resort to the smaller 5 Qubit Quantum Computer.

So for every run of my program, I would get 5 random bits. I can tell the Quantum Computer to execute my program 8192 in one run, so each run gives me 5 kB of random bytes.

Problem is that there is one Quantum Computer for everybody to share, so sometimes my program had to wait for 5 hours before it can run (as everybody has to wait their turn), so I wrote a little script that automates this over and over again. Then I let this run for at least 8 weeks (sorry IBM 😉 and I have collected around 15MB of random bytes from a real Quantum Computer…

That in itself tells you that this is not yet a viable way of producing random numbers, but let’s look at the quality of these numbers…

 

 Simulator

Just to make sure that I don’t have a bug in my program, I ran my Quantum Computing Program with a simulator locally on my laptop and the results are really cool.

As you can see, the distribution of the random bytes are quite nicely distributed between 0 and 255 (the numeric range of 1 byte), so that suggests that at least the distribution is really very nice.

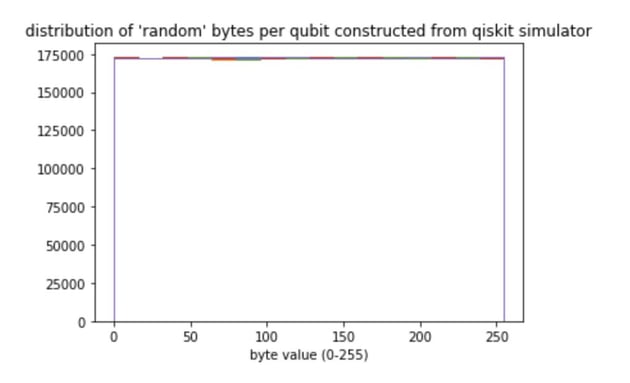
While the distribution looks awesome, it doesn’t really tell you whether the numbers are really random (ascending numbers from 0 to 255 would ensure that each number was only used once, this giving this a nice distribution, but it is completely non-random). In fact there is no easy way to tell you how good random numbers are, so I’m focusing on the distribution and in the simulator, this looks pretty good.

 

Real Quantum Computer

After letting run my program for the better part of 8 weeks and collecting around 15MB of random bytes from IBM’s Quantum Computer (and the surprise that they didn’t block my account yet ;-), here is the distribution of the random bytes from IBM’s ibmqx4 Quantum Computer

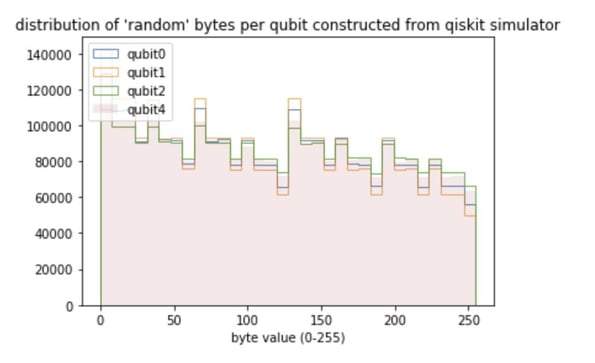
I have purposefully omitted the random numbers from qubit3 (see below for the reason behind this). But if you look at that distribution, this looks horrible and much, much worse than the beautiful picture from the simulation case. For example the “random number” 127 is produced almost twice as often as the number 121, which obviously shouldn’t be the case.

The reason for this is that current Quantum Computers are noisy and imperfect. I dedicated my last blog post to this topic.

Conclusion

So while theoretically Quantum Computers will give us perfect random numbers, in reality the random numbers from a Quantum Computer are pretty bad due to the noise level being way too high.

Right now, the noise kills a lot of the benefit of Quantum Computers and for that reason we have to take noise into account when designing algorithms on the current noisy Quantum Computers. (see one of my next posts on why this isn’t really a massive problem right now though for many applications)

One of the most active research area is the error correction where this noise level goes down substantially.

So while current Quantum Computers are quite noisy (as one can easily see), there is no question that over the next years, Quantum Computers will be dramatically better – both in terms of quantity as well as quality of the qubits.

So what happened to Qubit 3?

Well, to be honest, I don’t really know as well. If I look at the distribution of random bytes coming out of Qubit 3, it looks like this:

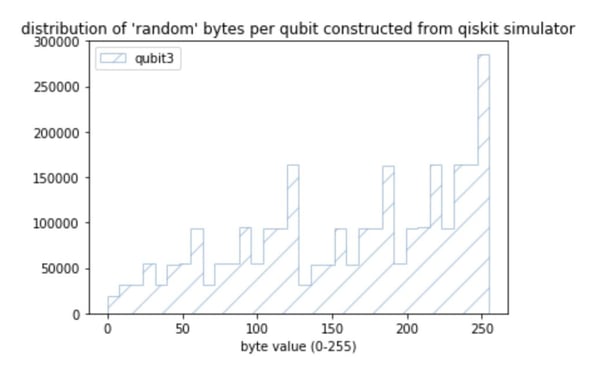
And wow, this looks completely different compared to the other 4 Qubits and it does indeed look very, very, very screwed up.

I’ve been in touch with members of the IBM team and they have acknowledged the issue and they have reproduced the issue and they “have some ideas what’s going on“, but unless I hear otherwise, it seems that I have inadvertently discovered a bug in IBM’s ibmqx4 Quantum Computer. This distribution cannot really be explained by noise or topology or anything else I can think of, so let’s wait and see what IBM says, but to have found a bug in a Quantum Computer would be very, very cool 😉

Qiskit code

For the interested reader, the Quantum Computer Program (using qiskit) to produce the random numbers is below.

The “main” work is in collecting the random numbers produced by each qubit separately as only then I was able to identify the anomaly with Qubit3, so in the program below, the first 1024 bytes are the random bytes from Qubit4, the second 1024 random bytes are from Qubit3 and so on…

Click here to view full code.

 Result files

I have ~3MB random bytes collected from each of the 5 qubits independently (in total around 15MB). I’m very happy to share the data with anyone who is interested. Just send me a note and I’ll send you the files. Email: ab@quintessencelabs.com

Andreas Baumhof, Vice President of Quantum Technologies