Quantum Computers and its possibilities are almost now a daily news item and while there is no doubt that Quantum Computers will revolutionize our traditional computers, we are not quite there yet. But not just in terms of the number of qubits (the biggest quantum computer has 72 qubits). The quality of these qubits are pretty bad too.

Don’t get me wrong, 72 qubits is a technological feast and while it sounds tiny, even these “tiny” quantum computers are almost big enough to demonstrate something called “Quantum Supremacy” – which means it can solve problems that classical computers practically cannot. That is a big statement. And I believe we are not that far from demonstrating this for some specialized applications. (I’ll focus on this in one of my next posts).

But if you believe some journalists who get overly excited by the possibilities (“Quantum Computers will break everything“), a quick reality check is needed and I’m hoping to give you a good practical introduction to this topic.

In an attempt to classify the current set of Quantum Computers, John Preskill coined the phrase “NISQ”, which means Noisy-Intermediate-Scale-Quantum Technology. He coined this to make it abundantly clear that current quantum computers are not yet universal machines.

So what does it mean that quantum computers are “noisy” and how “noisy” are they?

Qubits are the building blocks of quantum computers and as quantum effects only happen when its really small and really cold, these qubits are tiny and typically inside a big refrigerator operating close to absolute zero (-273 degree Celsius).

The problem is that we want these qubits to interact with each other (so we can do computations), but we don’t want these qubits to interact with the environment – except when we control or measure them.

We haven’t found a way yet to do this without interference and this interference introduces noise, which will be visible as errors when we do calculations (see below).

The other problem is that these qubits are not yet really stable, meaning they lose their quantum effects within milli-seconds and our calculations better be finished before that happens as otherwise the information is lost.

So how does this look like in reality?

So let’s write a little program. My program should flip a coin and if it is heads, it should print “00” and if it is tails, it should print “11”, simple right?

The program could look something like this:

from random import randint

# get random number between 0 and 1 and if it is 0 then print "00", otherwise "11"
if (randint(0,1) < 1):
   print ("00")
else:
   print ("11")

And indeed if we run this, the output looks something like this. Rouphly half the time it returned “00” and the other half “11”. Great.

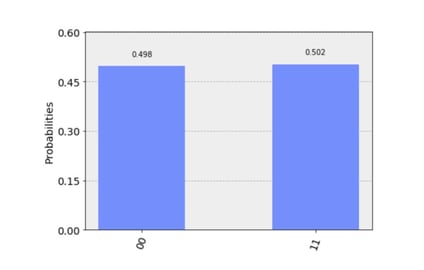
Cool, so let’s run this on a real quantum computer.

We’ll use IBM’s Quantum Computer. Now on a quantum computer we take two qubits, apply some quantum gates to it to guarantee that both qubits have the same value when we measure them (meaning either “00” or “11”). And they’ll have that in exactly 50% of the cases, so our quantum program matches exactly our little classical program above. I want to make it really clear that “00” and “11” are the only possible outcomes… nothing else (Bell State).

So what does the output from our quantum computer look like? Let’s see…

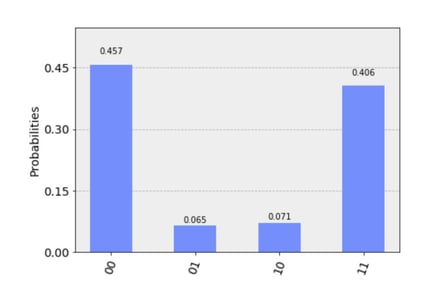
Err… Wow… What? “00” and “11” are almost equally distributed (although by far not 50/50) and I have in 6% the cases the result “01” and in 7% the cases the result “10”.

Problem is that these outcomes are not valid outcomes of my program and if my quantum computer would have no errors, these wouldn’t exist. But all current quantum computers are noisy and this noise will manifest itself in errors within the calculation. So the two case of “01” and “10” represent the error resulting from the noise in the system.

Now in the example above, I can still see that “00” and “11” are by far much more common, but “01” and “10” kind of represent the noise. And the fact that almost 13% of the results are outcomes that shouldn’t happen, tells you how noisy this computer is.

You may ask that if current quantum computers are so noisy for such simple computations, an anyone do anything useful with them yet?

The answer is absolutely, and we deliberately account for the noise in the mathematical models behind it, but what it means is that you can’t just blindly run a program on a quantum computer without understanding the topology of the backend or what type of quantum computer there is.

In the classical world, whe you write a code, you don’t have to worry whether it runs correctly on Windows, Mac, iPhone or Linux. It’ll run and spit out the same result. On quantum computers (or at least on the NISQ style quantum computers) you do need to worry about these details.

Error correction

If we don’t want to take the noisiness of the quantum system into account when we write our computations, we need to employ a technique called “error correction” and it is one of the most active area of research right now.

The basic idea is that if I can’t quite trust the outcome of one qubit, let’s take (say) 10 qubits and if not all 10 qubits agree, I simply take the majority vote. (very simplified). If we can eliminate the error, we talk about a “logical qubit” (no errors) vs a “physical qubit” (error). Current estimates assume that we’d need around 10-50 physical qubit for one logical qubit right now (that’ll change though)

Conclusion

There are actually three main areas quantum computing hardware focuses on and they are all equally important for real world applications

• number of qubits.
• reduce the error probability of qubits, gates and measurement
• stability of qubits

Andreas Baumhof, Vice President of Quantum Technologies