You’ve heard me rambling about Quantum Computers and the impact they will have on cryptography. Probably the biggest and most well-known impact is that they will be able to use Shor’s quantum algorithm to crack all RSA/ECC cryptography. Fortunately, Quantum Computers powerful enough to do this are not yet in sight, although that does not mean that we can relax…

Classical computers can do this too – it takes just a looooooooong time

Actually, you don’t need a quantum computer at all to crack RSA/ECC, if you have a lot of time that is. You can use a “normal” (read classical) computer as well. It is just unbelievably hard for this normal computer to solve this. It would take a classical computer around 300 trillion years to break a RSA-2048 bit encryption key. That’s why we all feel that we are “safe” from these attacks. But it does illustrate that the foundation of all of our cryptography is not guaranteed to be secure, it is only known to be really, really hard to solve (like trillion of years hard). That’s what we call “computational security”.

A perfect Quantum Computer could do this in 10 seconds

Now the trick with Shor’s algorithm is that he found a way to massively reduce the complexity of breaking RSA/ECC using a quantum computer. The problem that otherwise has exponential complexity (meaning if N is the number of bits, the N is in the exponent e.g. 5^N) gets reduced to polynomial complexity (meaning the N is in the base, e.g. only N^5). And that makes a massive difference. A quantum computer with 4099 perfectly stable qubits could break the RSA-2048 encryption in 10 seconds (instead of 300 trillion years – wow).

The problem is that such a quantum computer doesn’t exist (yet).

We have neither the number of qubits needed (4099), nor the quality of qubits (perfectly stable). The biggest quantum computer has currently 72 qubits (Google Bristlecone), however it has an error rate of 0.6%. The hardest problem though is coherence time. The coherence time is a measure of how fast the qubits lose their special quantum properties, so any calculation needs to finish within the coherence time. The coherence time at the moment is typically between 50-90 microseconds, so you can forget about any calculation that takes a while!

All of these issues obviously preclude anyone from running Shor’s algorithm on a Quantum Computer, and it is unclear when a powerful enough quantum computer will be available (maybe 5 years, maybe 10 years, maybe 20 years), so we can relax right?

Well, the problem is that innovation always comes in waves and sometimes breakthroughs are exactly that: they break through the established prediction. With the massive amount of research going into this field, it is hard to keep track of all the efforts.

So where are we really?

The most complete effort to highlight what’s possible has been published by Craig Gidney from Google and Martin Ekera from the Royal Institute of Technology in Stockholm. Just last month, they published a paper called “How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits“.

The most interesting part of this paper is that they derived a complete system taking the noisy/imperfect qubits into account with a gate error rate of 0.1%. IBM’s Q System One has a one-qubit gate error rate of 0.04% and an average two-qubit gate error rate of 1.6%, so we are not far off even with the current “noisy” quantum computers.

Now 20 million qubits is still a lot of qubits, but for the very first time we have an algorithm that is not just theoretical in nature (“If I assume a perfect quantum computer exists, then I can solve this“), but very practical (i.e. “we worked around the current limitations and with modest improvements on current architectures we can solve this“). This is a massive shift and I’m sure the 20 million qubits can be reduced quite a bit as well if the gate error rate is reduced and through other optimization.

The same result was determined to be achievable back in 2012 with 1 billion qubits (Fowler et al), then with 230m qubits in 2017 (O’Gorman et al), 170m qubits in 2019 with (Gheorghiu et al), taking us to the with 20m qubits in 2019 with the analysis described above (Gidney, Ekera). So we went from 1 billion qubits to 20m qubits in the space of 7 years. That’s what I mean when I talked about breakthroughs and massive research going into this field.

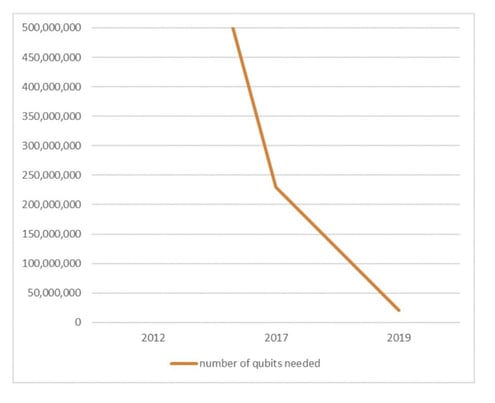
Now that’s all well and good, but even this research is “theoretical” since the authors obviously couldn’t run their algorithm on real quantum computing hardware (as this doesn’t exist yet).

So what can currently available hardware do?

Let’s first look at what’s possible on current classical computers. In 2010, researchers successfully factored a 768-bit integer (basically breaking RSA-768). That’s a number with 232 digits! They had to use many hundreds of machines over a timeframe of 2 years (!) It’ll be tough to compare this to a single quantum computer, but here we go.

So, what is the biggest number that has been factored by a quantum computer available today?

The biggest number to be factored is 35 [1], achieved on IBM’s Quantum Computer (https://arxiv.org/abs/1903.00768). 35 is a 6-bit number, so we are far away from 2048 bit RSA keys (which has 617 decimal digits – compared to these 2 digits!!!) In fact I’m sure most of you burst out laughing at this tiny number…

Now, what’s next?

Quantum Annealing

Well, while the world is pre-occupied about estimating when we will have universal quantum computers big enough and stable enough to run Shor’s algorithm, a new approach is emerging which could potentially be a much bigger risk to RSA and cryptography in general.

Quantum Annealing is emerging as a powerful force to be reckoned with. Quantum Annealing Devices (e.g. D-Wave’s Quantum Computer) are not universal quantum computers. They can’t calculate everything. They cannot run Shor’s algorithm. They can only solve special optimization problems, but because of these limitations, they have been around for a longer time, are much more mature and have many more qubits than universal quantum computers.

As it turns out, the problem of factoring integers can also be formulated as an optimization problem. A good introduction to this topic can be found in this paper by Raouf Dridi and Hedayat Alghassi (https://arxiv.org/abs/1604.05796). They were able to factor the number 200,099 in 2016 with 897 qubits.

Their algorithm ran successfully on D-Wave’s 2X Processor which has 1,100 qubits. That is already an 18-bit number.

But the biggest news came out of China when earlier this year, Chinese researchers from the Shanghai University broke this record by factoring the number 1,005,973 with only 89 qubits on D-Wave’s hardware. That is now already a 20-bit number.

Two things were very interesting about their approach.

• They were able to run this on currently available hardware, meaning the current quality of qubits is good enough to achieve these results. To factor a RSA-768 number (current factorization record on classical computers), their algorithm would “only” need 147,454 qubits. D-Wave have announced a quantum computer with 5,640 qubits already, so the more qubits there are, the more vulnerable RSA will become.
• Their algorithm uses a combination of quantum and classical computation to maximise the results. (interestingly that’s the same for Shor’s algorithm and a common approach. Use classical computers for what they are good at and quantum computers for what they are good at)

If we assume a doubling of the quantum annealing qubits every 2 years (which was the case in the past), we’ll be there in 10 years. To me it seems much more likely to achieve this goal versus the alternative route of building 1,539 logical qubits on a perfect error-free universal quantum computer to allow it to run Shor’s algorithm in 10 years.

These time estimates assume that no fundamental breakthrough from an algorithmic side will be made and the same algorithm will be run on a D-Wave device just with more qubits. This is obviously a massive simplification as there is so much research happening at the moment, which will inevitably lead to breakthroughs. In addition, it’s not just the number of qubits, but also better inter-connectivity which will further reduce the required qubits.

Funnily, Mahatma Gandhi’s quote fits this perfectly: “First they ignore you (Quantum Computers will never exist), then they laugh at you (really, you can factor the number 35? Cool…), then they fight you, then you win”.

So, time to strap in to enjoy the next years of innovation in this area 🙂

[1] There are shortcuts for special cases (e.g. when the two prime factors only differ by a little bit) and then 966,887 is the highest number that was factored, but these special cases don’t help breaking RSA, so we do not count these cases.